II. 4. Apollonio di Perga
Durante il primo secolo dell'Età ellenistica tre matematici
eccelsero su tutti gli altri del loro tempo e anche sulla maggior
parte di coloro che li precedettero e seguirono: Euclide,
Archimede e Apollonio.
Di Apollonio si sa che era nato a Perga, in Pamfilia, e che aveva
ricevuto la sua educazione scientifica ad Alessandria. Per un
certo periodo visse anche a Pergamo, dove c'era una Accademia e
una biblioteca che in ordine di importanza veniva immediatamente
dopo quella del Museo di Alessandria. Non conosciamo con
esattezza le date della sua vita, ma la tradizione riferisce che
egli fu attivo durante i regni di Tolomeo Evergete e Tolomeo
Filipatore: è stata avanzata l'ipotesi che sia vissuto dal 262
al 190 a.C..
L'opera che ha fatto sì che Apollonio diventasse noto come
"il Grande Geometra" è intitolata le Coniche.
 |
Frontespizio dell'opera in un'edizione del 1710. |
Di questo trattato in otto libri, solo i primi quattro sono
pervenuti nel testo originale greco; i tre successivi invece sono
giunti a noi tramite una traduzione araba.
Le sezioni coniche erano già note da un secolo e mezzo quando
Apollonio compose questo celebre trattato su queste curve, ma
nessuna opera precedente (neppure le Coniche di Euclide)
aveva raggiunto un livello così alto.
Il Libro I si apre con una esposizione delle motivazioni che
avevano portato l'autore a scrivere l'opera. Mentre si trovava ad
Alessandria, Apollonio era stato visitato da un geometra di nome
Neucrate e fu per le sue sollecitazioni che Apollonio buttò giù
una versione affrettata delle Coniche in otto libri.
Più tardi, a Pergamo, l'autore ebbe il tempo di perfezionare
ogni libro e per questo i Libri IV e VII si aprono con dediche ad
Attalo, re di Pergamo. L'autore considera i primi quattro libri
una introduzione elementare e perciò si è avanzata l'ipotesi
che gran parte del loro contenuto fosse già apparso in
precedenti trattati. Gli ultimi quattro libri vengono descritti
da Apollonio come ulteriori sviluppi degli argomenti al di là
degli elementi essenziali.
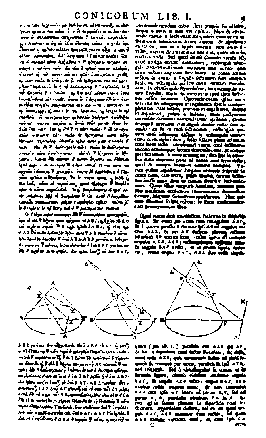
Prima di Apollonio l'ellisse, la parabola e l'iperbole venivano
costruite come sezioni di tre tipi nettamente distinti di coni
circolari retti, a seconda che l'angolo al vertice fosse acuto,
retto o ottuso. Apollonio, per la prima volta, dimostrò che non
era necessario prendere sezioni perpendicolari ad un elemento del
cono e che da un unico cono era possibile ottenere tutte e tre le
varietà di sezioni coniche semplicemente variando l'inclinazione
del piano di intersezione. Una seconda importante
generalizzazione si ebbe quando Apollonio dimostrò che non era
necessario che il cono fosse un cono retto (cioè un cono il cui
asse è perpendicolare alla base), ma che poteva essere anche un
cono circolare obliquo o scaleno. Infine, Apollonio avvicinò
ulteriormente le antiche curve al punto di vista moderno
sostituendo il cono a una falda con un cono a doppia falda.
Infatti, Apollonio dava la stessa definizione che viene usata
ancora oggi di cono
circolare [39]:
Se una retta, prolungantesi all'infinito e passante sempre per un punto fisso, viene fatta ruotare lungo la circonferenza di un cerchio che non si trovi nello stesso piano del punto in modo che passi successivamente attraverso ogni punto di quella circonferenza, la retta che ruota traccerà la superficie di un cono doppio.
Questo cambiamento fece sì che l'iperbole assumesse la forma
di quella curva a due rami che ci è oggi familiare. I matematici
antichi parlavano spesso di "due iperboli" piuttosto
che di "due rami" di un'unica iperbole, ma in entrambi
i casi si riconosceva la duplicità della curva.
Fu Apollonio ad introdurre i termini "ellisse",
"iperbole" e "parabola" in relazione alle sezioni
coniche [40]: essi rappresentavano adattamenti di termini che
erano già stati usati precedentemente nella soluzione delle
equazioni di secondo grado mediante l'applicazione di aree.
Il Libro II contiene lo studio (anticipato nel Libro I) dei diametri coniugati e delle tangenti.
Sembra che Apollonio fosse orgoglioso del Libro III. Infatti nella prefazione generale alle Coniche scriveva:
Il Libro III contiene molti teoremi notevoli, utili per la sintesi dei luoghi solidi e per la determinazione dei limiti; la maggior parte di essi, e i più belli, sono nuovi. Quando li scopersi, mi resi conto che Euclide non aveva effettuato la sintesi del luogo geometrico rispetto a tre o quattro linee, ma soltanto quella di una parte di tale luogo geometrico, e ciò in maniera casuale e poco felice: non era infatti possibile effettuare la sintesi completa senza queste mie nuove scoperte.
Il luogo geometrico rispetto a tre o quattro rette svolge un ruolo importante nella matematica da Euclide fino a Newton. Date tre rette giacenti in un piano si deve trovare il luogo geometrico di un punto P che si muove in modo che il quadrato della distanza di P da una di queste rette sia proporzionale al prodotto delle distanze delle altre rette (o, nel caso di quattro rette, il prodotto delle distanze da due di esse sia proporzionale al prodotto delle distanze dalle altre due), ove le distanze vengono misurate secondo angoli dati rispetto alle rette. Usando i metodi analitici moderni è facile mostrare che il luogo geometrico in questione è una sezione conica, reale o immaginaria, riducibile o irriducibile. Il nostro metodo di risoluzione non dà, però, una idea adeguata del modo in cui Apollonio tratta il problema del Libro III, dove più di cinquanta proposizioni accuratamente formulate verbalmente, tutte dimostrate con metodi sintetici, portano alla fine al luogo geometrico desiderato. Mezzo millennio più tardi Pappo suggerì una generalizzazione di questo teorema per n linee con n>4. Fu affrontando questo problema generalizzato che Descartes nel 1637 mise alla prova la sua geometria analitica.
Descrivendo il contenuto del Libro IV delle Coniche, Apollonio dice che esso mostra "in quanti modi le sezioni coniche possono incontrarsi l'una con l'altra", e si dichiara particolarmente fiero dei teoremi "nessuno dei quali era stato discusso da autori precedenti", concernenti il numero di punti in cui la sezione di un cono incontra i rami opposti di una iperbole.
La prefazione del Libro V, che tratta dei segmenti massimi e minimi che si possono tracciare rispetto ad una conica, ripete che "l'argomento è uno di quelli che sembrano degni di essere studiati per se stessi".
Dedicando il Libro VI delle Coniche al re Attalo, Apollonio lo descriveva come un libro che abbracciava proposizioni concernenti "segmenti di coniche uguali e disuguali, simili e dissimili, oltre ad altre questioni trascurate da coloro che sono venuti prima di me. In particolare, troverai in questo libro come intersecare, in un cono retto dato, una sezione che sia uguale a una sezione data". Due coniche si dicono simili se le ordinate tracciate all'asse a distanze proporzionali dal vertice, sono rispettivamente proporzionali alle ascisse corrispondenti. Fra le proposizioni più facili del Libro VI vi sono quelle che dimostrano che tutte le parabole sono simili (Prop. 11) e che una parabola non può essere simile a una ellisse o a una iperbole, né una ellisse a una iperbole (Prop. 14, 15). Altre proposizioni (26, 27) dimostrano che se un cono qualsiasi viene intersecato da due piani paralleli formando sezioni iperboliche o ellittiche, le sezioni saranno simili ma non uguali.
Il Libro VII ritorna sull'argomento dei diametri coniugati e contiene "molte nuove proposizioni concernenti diametri di sezioni e le figure descritte su di essi". Fra queste ve ne sono alcune che si trovano anche nei manuali moderni, come la dimostrazione (Prop.12, 13, 29,30) che
in ogni ellisse la somma, e in ogni iperbole la differenza, dei quadrati costruiti su due diametri coniugati qualsiasi, è uguale alla somma, rispettivamente alla differenza, dei quadrati costruiti sugli assi.
E' stata fatta la congettura che il Libro VIII, perduto, delle Coniche non facesse che continuare la trattazione di problemi simili: infatti nella prefazione al Libro VII l'autore scriveva che i teoremi di tale libro sarebbero stati usati nell'ottavo per risolvere problemi conici, così che l'ultimo libro è una sorta di appendice.
Nonostante la sua enorme produzione scientifica, solo un altro tra i numerosi trattati di Apollonio è pervenuto in forma quasi completa. Tutte le versioni greche della Sezione di un rapporto andarono perdute molto tempo fa, ma non prima che fosse stata fatta una traduzione araba. Essa tratta vari casi di un problema generale: date due rette e un punto su ciascuna di esse, tracciare per un terzo punto dato una retta che intersechi sulle rette date segmenti (misurati a partire dai punti fissi rispettivamente giacenti su di esse) che siano in un dato rapporto.
Attraverso le descrizioni fornite da Pappo e da altri commentatori posteriori, conosciamo il titolo di molte opere andate perdute:
Il problema trattato è simile a quello della Sezione di un rapporto, tranne che i segmenti intersecati devono delimitare un dato rettangolo, piuttosto che essere in un dato rapporto. Questo problema porta alla costruzione, su un segmento a, di un rettangolo uguale a un rettangolo più un quadrato.
Tratta quella che potremmo chiamare geometria analitica ad una dimensione. Esso considera il seguente problema generale: dati quattro punti A, B, C, D, giacenti su una retta, determinare il quinto punto P giacente su di essa tale che il rettangolo delimitato dai segmenti AP e CP stia in un dato rapporto con il rettangolo delimitato dai segmenti BP e DP.
Presenta il problema noto come il "Problema di Apollonio". Date tre cose, ciascuna delle quali può essere un punto, una retta o un cerchio, tracciare un cerchio che sia tangente a ciascuna delle tre cose. Questo problema comporta dieci casi, dai due più facili in cui le tre cose sono tre punti o tre rette a quello più difficile in cui le tre cose sono tre cerchi (si veda a questo proposito il sito Il punto di Apollonio [41]).
Apollonio considerava la classe dei problemi di neusis (inclinazione) che potevano essere risolti con metodi "piani", ossia solo per mezzo di riga e compasso. Un esempio è fornito dalla trisezione dell'angolo [42].
Tra i luoghi considerati vi erano: il luogo dei punti tali che la differenza dei quadrati delle loro distanze da due punti fissi sia costante è una retta perpendicolare al segmento che congiunge i punti; il luogo dei punti tali che il rapporto delle loro distanze da due punti fissi sia costante (e diverso da uno) è un cerchio. Quest'ultimo luogo è oggi noto come il "Cerchio di Apollonio".